FK arm
A Forward Kinematics calculation of a 5-axis arm
Method 1
Use a loop function to calculate the matrix
#include <iostream>
#include <cmath>
using namespace::std;
double alpha[5] = {0,M_PI/2,0,0,0};
double theta[5] = {0,0,0,0,0};
double a[5] = {0,0,105,90,65};
double d[5] = {16,0,0,0,0};
double rot[5] = {theta[0],M_PI/2-theta[1],theta[2],-theta[3],theta[4]};
double matrixW[4][4] = {
{1,0,0,0},
{0,1,0,0},
{0,0,1,0},
{0,0,0,1}
};
void multiply(double trans[][4], double mat1[][4], double result[][4]) {
for(int i = 0; i < 4; ++i) {
for(int j = 0; j < 4; ++j) {
double sum = 0;
for(int k = 0; k < 4; ++k) {
sum += mat1[i][k] * trans[k][j];
}
result[i][j] = sum;
}
}
}
void calculateW(){
for(int i = 4; i > -1; i--){
double trans[4][4] =
{{cos(rot[i]), -sin(rot[i]), 0, a[i]},
{sin(rot[i])*cos(alpha[i]), cos(rot[i])*cos(alpha[i]), -sin(alpha[i]), -sin(alpha[i])*d[i]},
{sin(rot[i])*sin(alpha[i]), cos(rot[i])*sin(alpha[i]), cos(alpha[i]), cos(alpha[i])*d[i]},
{0, 0, 0, 1}};
double result[4][4];
multiply(matrixW, trans, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrixW[i][j] = result[i][j];
}
}
}
}
int main() {
cout<< "W"<<"\n";
calculateW();
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
if(abs(matrixW[i][j])<0.001){
matrixW[i][j] = 0;
}
cout << matrixW[i][j] << "\t" << "\t";
}
cout<< "\n";
}
return 0;
}
Method 2
Add Y-axis rotation
Although we never thought about add y-axis rotation in DH, I consider Y-axis rotation as a possibility of the solution for joint 1 and joint 5
- Principle
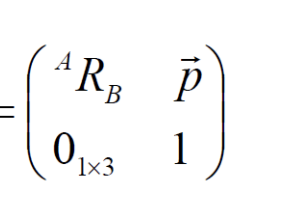
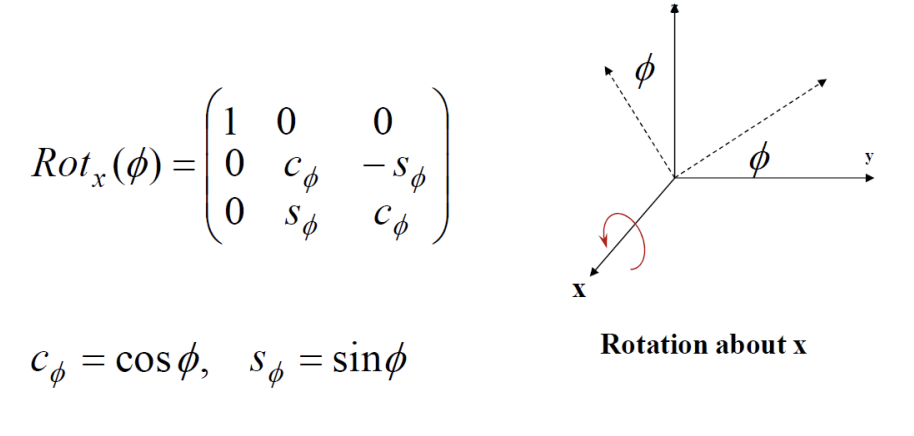
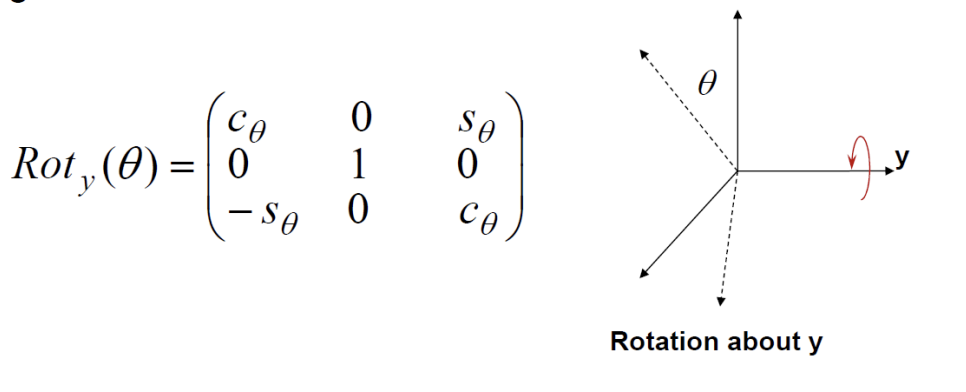
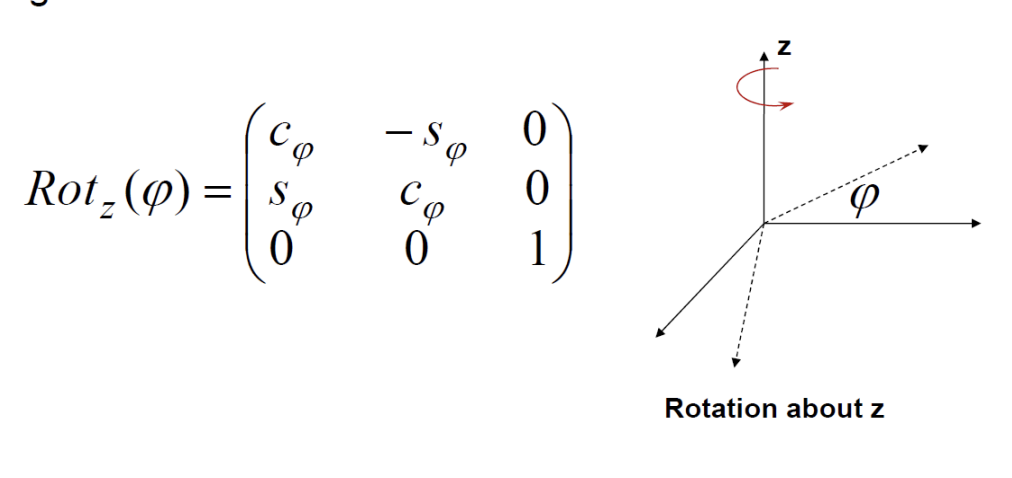

- code
#include <iostream>
#include <cmath>
using namespace std;
/**************************************************/
double a[5] = {0,16,105,90,0};
/**************************************************/
double alfa[5] = {0,0,0,0,0};
/**************************************************/
double d[5] = {0,0,0,0,65};
/**************************************************/
double rot[5] = {0,0,0,0,0};
/**************************************************/
double beta[5] = {-M_PI/2,0,0,M_PI/2,0};
/**************************************************/
double matrix[4][4] =
{{1, 0, 0, 0},
{0, 1, 0, 0},
{0, 0, 1, 0},
{0, 0, 0, 1}};
void multiply(double mat1[][4], double trans[][4], double result[][4]) {
for(int i = 0; i < 4; ++i) {
for(int j = 0; j < 4; ++j) {
double sum = 0;
for(int k = 0; k < 4; ++k) {
sum += mat1[i][k] * trans[k][j];
}
result[i][j] = sum;
}
}
}
void trans(int index){
double result[4][4];
double roty[4][4] = {
{cos(beta[index]),0,sin(beta[index]),0},
{0,1,0,0},
{-sin(beta[index]),0,cos(beta[index]),0},
{0,0,0,1}
};
multiply(roty, matrix, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrix[i][j] = result[i][j];
}
}
double rotz[4][4] = {
{cos(rot[index]),-sin(rot[index]),0,0},
{sin(rot[index]),cos(rot[index]),0,0},
{0,0,1,0},
{0,0,0,1}
};
multiply(rotz, matrix, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrix[i][j] = result[i][j];
}
}
double transz[4][4] = {
{1,0,0,0},
{0,1,0,0},
{0,0,1,d[index]},
{0,0,0,1}
};
multiply(transz, matrix, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrix[i][j] = result[i][j];
}
}
double rotx[4][4] = {
{1,0,0,0},
{0,cos(alfa[index]),-sin(alfa[index]),0},
{0,sin(alfa[index]),cos(alfa[index]),0},
{0,0,0,1}
};
multiply(rotx, matrix, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrix[i][j] = result[i][j];
}
}
double transx[4][4] = {
{1,0,0,a[index]},
{0,1,0,0},
{0,0,1,0},
{0,0,0,1}
};
multiply(transx, matrix, result);
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
matrix[i][j] = result[i][j];
}
}
}
void calculate(){
for(int i = 4; i > -1; i--){
trans(i);
}
}
int main() {
//full_calculate();
calculate();
for(int i = 0; i < 4; i ++){
for(int j = 0; j < 4; j ++){
if(abs(matrix[i][j])<0.001){
matrix[i][j] = 0;
}
cout << matrix[i][j] << "\t" << "\t";
}
cout<< "\n";
}
return 0;
}
This time, I change the rotation on x-axis to y-axis in joint 1 and joint 5
Although the results for 1,2,3,4,5 and M_PI/4,-M_PI/6,M_PI/6,M_PI/4,M_PI/2 is different from the integrated matrix, but I believe it is the previous result incorrect
To make sure this approach is correct, I continued to try some combinations
| Rotation angle | End coordinates | Previous solution |
|---|---|---|
| 0,0,0,0,0 | 0,0,276 | 276,0,0 |
| 0,0,0,M_PI/2,0 | 0,65,211 | 122,0,-155 |
| M_PI/2,0,0,M_PI/2,0 | -65,0,211 | 0,122,-155 |
| M_PI/4,0,0,M_PI/2,0 | -46,46,211 | 86,86,-155 |
| 0,0,M_PI/2,M_PI/2,0 | 0,90,65 | -139,0,-155 |
| 0,0,-M_PI/2,M_PI/2,0 | ||
Theoretically, these values are correct, we can examine it if we have the robot arm